Mathematics Program Presents
Seating Arrangements, Domino Tilings, and Graph Factorials
Thursday, April 27, 2017
Hegeman 308
4:45 pm EDT/GMT-4
4:45 pm EDT/GMT-4
Amir Barghi, Mathematics Program
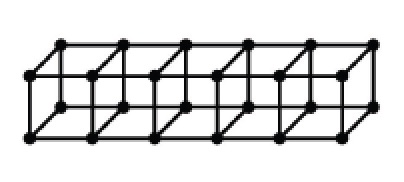
At a dinner party, each guest is assigned a seat along a long table, which seats 12 people. However, when all guests arrive, they decide to change things a little up by swapping seats. In order to minimize the amount of chaos, they have to follow the following three rules: a guest can keep their seat; two guests sitting next to each other or across the table can swap seats; three or more guests can swap seats in a cyclicfashion, provided that each person is moving one seat to the left or to the right or across the table. Assuming that all guests have showed up, how many possible seating rearrangements are there? Now consider the graph on the left. We want to place dominoes along some of the edges of this graph so that each vertex is covered by exactly one domino. We call any such placement of dominoes a domino tiling. How many domino tilings of this graph exits?
In this talk, we will explore the connection between these two problems by defining what the factorial of a graph is.
Prerequisites: A familiarity with graphs and counting arguments is a plus, but not
required.
For more information, call 845-758-7104, or e-mail [email protected].
Time: 4:45 pm EDT/GMT-4
Location: Hegeman 308